Rotation Matrices » Cleve’s Nook: Cleve Moler on Arithmetic and Computing

The homogeneous coordinates system utilized in at the moment’s pc graphics software program and {hardware} makes it doable to explain rotations, translations and plenty of different operations with 3-by-3 and 4-by-4 matrices. These matrices function on vectors with the place of an object, x, y and z , within the first three parts.

Rotations in regards to the coordinate axes are described by three matrices. Rotations in regards to the x -axis are produced by $R_x$, which rotates y and z, whereas leaving x unchanged.

$$ R_x(theta) = left( start{array}{rrr}
1 & 0 & 0
0 & cos{theta} & -sin{theta}
0 & sin{theta} & cos{theta}
finish{array} proper) $$

Rotations in regards to the y -axis are generated by

$$ R_y(theta) = left( start{array}{rrr}
cos{theta} & 0 & -sin{theta}
0 & 1 & 0
sin{theta} & 0 & cos{theta}
finish{array} proper) $$

And, rotations about z are offered by

$$ R_z(theta) = left( start{array}{rrr}
cos{theta} & -sin{theta} & 0
sin{theta} & cos{theta} & 0
0 & 0 & 1
finish{array} proper) $$

Rotation angles are laid out in levels. Our MATLAB packages use the degree-based trig features cosd and sind. Listed here are graphs of $costheta$ and $-sintheta$ , evaluated with the angle $theta$ going from 0 to 360 levels in 10-degree steps.

Right here is one other take a look at the identical information, cosd(theta) and -sind(theta) for theta = 0:10:360. The columns of the rotation matrix are the coordinates of the rotating dots. The blue dot begins at (0,1) and the orange dot begins at (1,0).

For those who drop the zeros from the values of theta, you might be left with the integers from 1 to 36. That is the numbering within the worldwide customary describing the compass course of runways at airports. The preliminary place of our blue dot corresponds to runway 36 and the orange dot begins as runway 9.

Word: Refresh your browser to synchronize these animations.

For plane and area automobiles, rotation across the x-axis from nostril to tail is called roll.

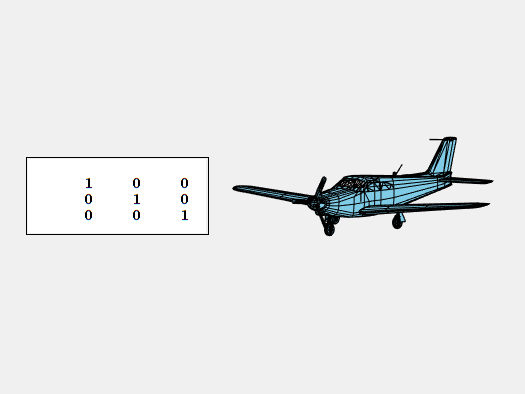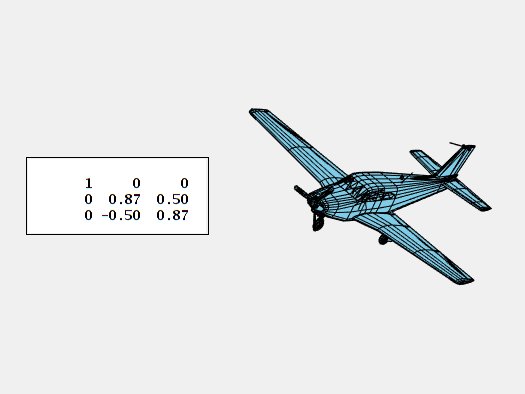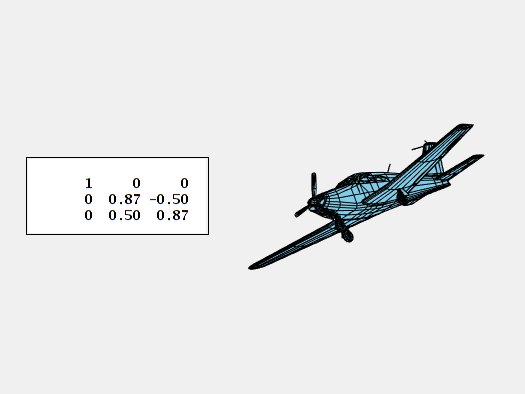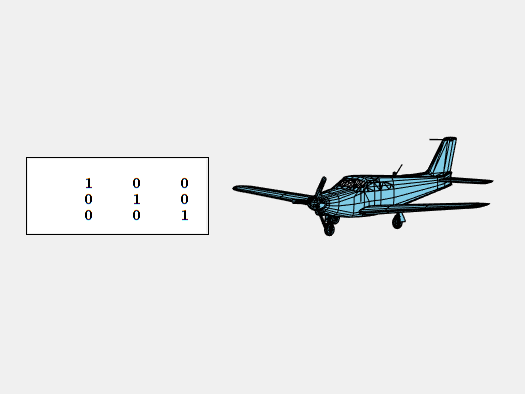
Rotation in regards to the y-axis parallel to the wings is pitch.

And, rotation in regards to the vertical z-axis is yaw.

Our mannequin of the Piper PA-24 Comanche has 97 patches. Considered one of them is the propeller. This animation of a rotating propeller is similar to our earlier animation of the compass.

Qube, our digital Rubik’s Dice simulator, makes use of 27 copies of a single cubelet. This animation of a rotating cubelet exhibits 1 / 4 flip clockwise about x, adopted by 1 / 4 flip clockwise about y after which 1 / 4 flip counterclockwise about z. If these three rotations are repeated 4 instances, the cubelet returns to its preliminary orientation. Within the course of, we see the standard Rubik’s colours of all six faces — white, inexperienced and orange reverse yellow, blue and pink.

Word: Refresh your browser to synchronize these animations.

Rubick’s Dice is all about rotations. Rotating the cubelets in any face of the puzzle, whereas leaving the remainder of the puzzle mounted, is known as a “transfer”. Like all dice, Rubik’s dice has six faces. Every transfer rotates one of many six faces in both a clockwise or counterclockwise course. So, after n strikes, the puzzle is in one in every of 12^n doable states. The problem is to return the dice to its unique orientation.

Listed here are six random rotations produced by scramble(6). As a result of 12^6 is 2,985,984, this is only one of virtually three million six-move scrambles.

One doable technique to restore any beginning situation is to retrace the strikes that produced it. That is the “comply with the breadcrumbs” algorithm. So, I name this unscramble, fairly than remedy.