Six: All of this has occurred earlier than.
Baltar: However the query stays, does all of this should occur once more?
Six: This time I guess no.
Baltar: , I’ve by no means identified you to play the optimist. Why the change of coronary heart?
Six: Arithmetic. Legislation of averages. Let a fancy system repeat itself lengthy sufficient and finally one thing shocking may happen. That, too, is in God’s plan.
Battlestar Galactica *
Momentum with cyclical step-sizes has been proven to typically speed up convergence, however why? We’ll take a more in-depth have a look at this method, and with the assistance of polynomials unravel a few of its mysteries.
$$
defaa{boldsymbol a}
defrr{boldsymbol r}
defAA{boldsymbol A}
defHH{boldsymbol H}
defEE{mathbb E}
defII{boldsymbol I}
defCC{boldsymbol C}
defDD{boldsymbol D}
defKK{boldsymbol Okay}
defeeps{boldsymbol varepsilon}
deftr{textual content{tr}}
defLLambda{boldsymbol Lambda}
defbb{boldsymbol b}
defcc{boldsymbol c}
defxx{boldsymbol x}
defzz{boldsymbol z}
defuu{boldsymbol u}
defvv{boldsymbol v}
defqq{boldsymbol q}
defyy{boldsymbol y}
defss{boldsymbol s}
defpp{boldsymbol p}
deflmax{L}
deflmin{mu}
defRR{mathbb{R}}
defTT{boldsymbol T}
defQQ{boldsymbol Q}
defCC{boldsymbol C}
defEcond{boldsymbol E}
DeclareMathOperator*{argmin}{{arg,min}}
DeclareMathOperator*{argmax}{{arg,max}}
DeclareMathOperator*{reduce}{{reduce}}
DeclareMathOperator*{dom}{mathbf{dom}}
DeclareMathOperator*{Repair}{mathbf{Repair}}
DeclareMathOperator{prox}{mathbf{prox}}
DeclareMathOperator{span}{mathbf{span}}
defdefas{stackrel{textual content{def}}{=}}
defdif{mathop{}!mathrm{d}}
definecolor{colormomentum}{RGB}{27, 158, 119}
definecolor{colorstepsize1}{RGB}{217,95,2}
definecolor{colorstepsize2}{RGB}{117,112,179}
definecolor{colorstepsize}{RGB}{152,78,163}
defmom{{coloration{colormomentum}m}}
defstepzero{{coloration{colorstepsize1}h_0}}
defstepone{{coloration{colorstepsize2}h_1}}
deftildestepzero{{coloration{colorstepsize1}tilde{h}_0}}
deftildestepone{{coloration{colorstepsize2}tilde{h}_1}}
defmomt{{coloration{colormomentum}m_t}}
defht{{coloration{colorstepsize}h_t}}
defstept{{coloration{colorstepsize}h_t}}
defstep{{coloration{colorstepsize}h}}
definecolor{colorexternaleigenvalues}{RGB}{152, 78, 163}
definecolor{colorinternaleigenvalues}{RGB}{77, 175, 74}
defmuone{{coloration{colorexternaleigenvalues}{mu}_1}}
defLone{{coloration{colorinternaleigenvalues}{L}_1}}
defmutwo{{coloration{colorinternaleigenvalues}{mu}_2}}
defLtwo{{coloration{colorexternaleigenvalues}{L}_2}}
$$
Cyclical Heavy Ball
The commonest variant of stochastic gradient descent makes use of a continuing or lowering step-size. Nevertheless, some current works advocate as an alternative for cyclical step-sizes, the place the step-size alternates between two or extra values.
The scheme that we’ll think about has two step-sizes $stepzero, stepone$, in order that odd iterations use one step-size whereas even iterations use a special one.
Cyclical Heavy Ball
Enter: beginning guess $xx_0$, step-sizes $0 leq stepzero leq stepone$ and momentum ${coloration{colormomentum} m} in [0, 1)$.
$xx_1 = xx_0 – dfrac{stepzero}{1 + {color{colormomentum} m}} nabla f(xx_0)$
For $t=1, 2, ldots$
begin{align*}label{eq:momentum_update}
&text{${color{colorstepsize}h_t} = stepzero$ if $t$ is even and ${color{colorstepsize}h_t} = stepone$ otherwise}
&xx_{t+1} = xx_t – {color{colorstepsize}h_t} nabla
f(xx_t)+ {color{colormomentum} m}(xx_{t} – xx_{t-1})
end{align*}
By alternating between a small and a large step-size, the cyclical step-size algorithm has very different dynamics than the classical constant step-size variant:
In both cases the parameters are set to those that maximize the asymptotic worst-case rate, assuming an imperfect lower and upper bound on the Hessian eigenvalues.
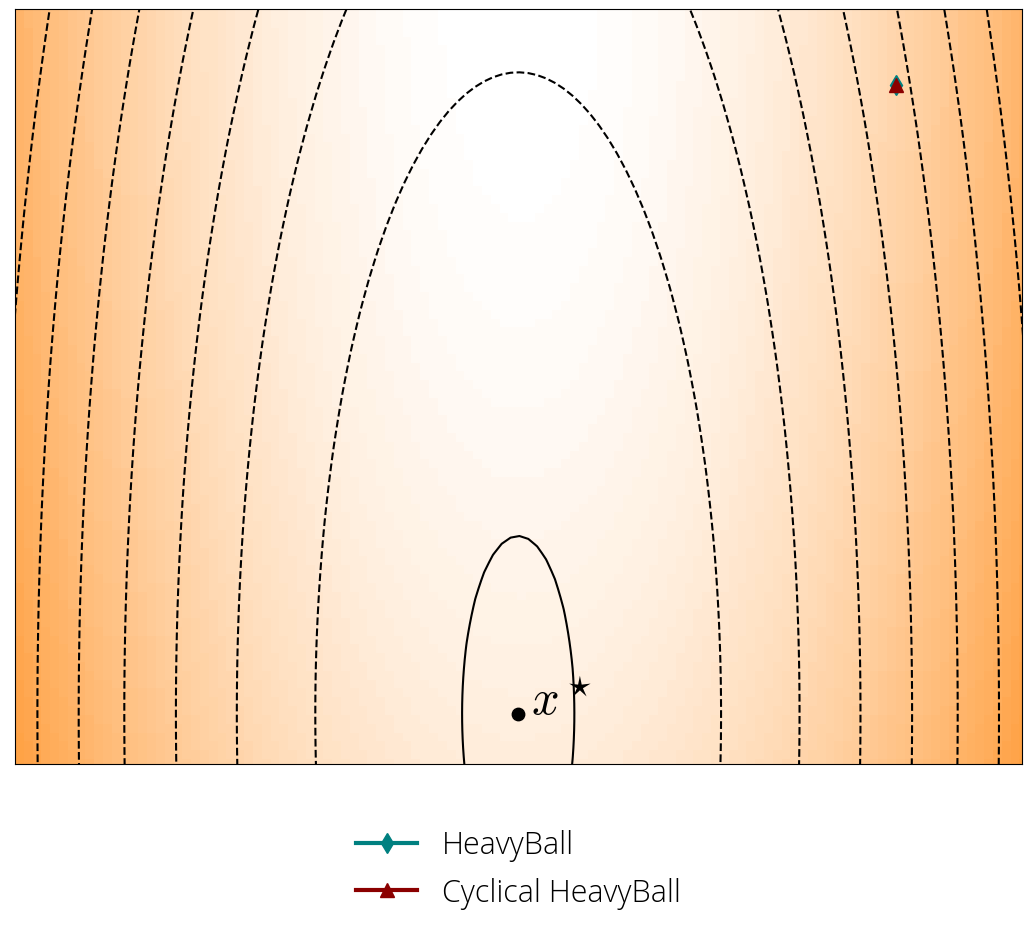
In this post, we’ll show that not only the cyclical heavy-ball can reach the same convergence as optimal
first-order methods such as Polyak and Nesterov momentum, but it can in fact achieve a faster convergence in some scenarios.
As in previous posts, the theory of orthogonal polynomials will be our best ally throughout the journey. We’ll start by expressing the residual polynomial of the cyclical heavy ball method as a convex combination of Chebyshev polynomials of the first and second kind (Section 2), and then we’ll use properties of Chebyshev polynomials to derive the worst-case optimal set of parameters (Section 3).
This post is based on a recent paper with the incredible Baptiste Goujaud, Damien Scieur, Aymeric Dieuleveut, and Adrien Taylor.
Related work
Very related to our paper is the recent work of Oymak.one large, $K-1$ small
steps instead of the alternating scheme that’s the subject of this post. He showed improved convergence rates of that scheme under the same eigengap assumption we’ll describe later. One important difference is that (Oymak 2021) doesn’t achieve the optimal rate on general strongly convex quadratics (see Appendix E.5
Chebyshev Meets Cyclical Learning Rates
As in previous blog posts in this polynomials series, we’ll assume our objective function $f$ is a quadratic of the form
begin{equation}label{eq:opt}
f(xx) defas frac{1}{2}xx^top HH xx + bb^top xx + c~,
end{equation}
where $HH$ is a $dtimes d$ positive semi-definite matrix with eigenvalues in some set $Lambda$.
As we saw in Part 2 of this series, with any gradient-based method we can associate a residual polynomial $P_t$ that will determine its convergence behavior.
begin{equation}
|xx_t – xx^star| leq {color{purple}underbrace{vphantom{max_{[L]}}max_{lambda in Lambda
}}_{textual content{conditioning}}} ,
{coloration{teal}underbrace{vphantom{max_{[L]}}|P_t(lambda)|}_{textual content{algorithm}} } ,,
{coloration{brown}underbrace{vphantom{max_{[L]}}|xx_0 – xx^star|}_{textual content{initialization}}}~.
finish{equation}
This inequality highlights the significance of with the ability to certain the residual polynomial,
Let $P_{t}$ denote the residual polynomials related to the cyclical heavy ball methodology at iteration $t$. By our definition of the residual polynomial in Half 1, the sequence of residual polynomials admits the recurrence
start{equation}
start{aligned}
&P_{t+1}(lambda) = (1 + mother – {coloration{colorstepsize}h_{bmod(t, 2)}} lambda) P_{t}(lambda) – mother P_{t-1}(lambda)
&P_0(lambda) = 1,,quad P_1(lambda) = 1 – frac{stepzero}{1 + mother}lambda,.
finish{aligned}label{eq:residual_cyclical_recurrence}
finish{equation}
What makes this recurrence totally different than different’s we’e seen earlier than is that the phrases that multiply the earlier polynomials rely upon the iteration quantity $t$ by way of the step-size ${coloration{colorstepsize}h_{bmod(t, 2)}}$ .
This is sufficient to break the earlier proof approach.
Fortunately, we will eradicate the dependency on the iteration quantity by chaining iterations in a method that the recurrence jumps two iterations as an alternative of 1.
Evaluating the earlier equation at $P_{2t + 2}$ and fixing for $P_{2t + 1}$ offers
start{equation}
P_{2t + 1}(lambda) = frac{P_{2t + 2}(lambda) + mother P_{2t}(lambda)}{1 + mother – steponelambda},.
finish{equation}
Utilizing this to interchange $P_{2t+1}$ and $P_{2t-1}$ within the unique recurrence eqref{eq:residual_cyclical_recurrence} offers
start{equation}
frac{P_{2t + 2}(lambda) + mother P_{2t}(lambda)}{1 + mother – steponelambda} = (1 + mother – stepzero lambda) P_{2t}(lambda) – mother left(frac{P_{2t}(lambda) + mother P_{2t-2}(lambda)}{1 + mother – steponelambda} proper),,
finish{equation}
which fixing for $P_{2t + 2}$ lastly offers
start{equation}label{eq:recursive_formula}
P_{2t + 2}(lambda) = left( (1 + mother – stepzerolambda)(1 + mother – stepone lambda) – 2 mother proper) P_{2t}(lambda) – mother ^2 P_{2t – 2}(lambda),.
finish{equation}
This recurrence expresses $P_{2t+2}$ when it comes to $P_{2t}$ and $P_{2t – 2}$. It is therefore a recurrence for less than even iterations, however it has one enormous benefit with respect to the earlier one: the coefficients that multiply the earlier polynomials now do not rely upon the iteration quantity.
As soon as now we have this recurrence, following an analogous proof to the one we did in Half 2, we will derive an expression for the residual polynomial $P_{2t}$ primarily based on Chebyshev polynomials of the primary and second form. That is helpful as a result of it’s going to later make it straightforward to certain this polynomial –and develop convergence charges– utilizing identified bounds for Chebyshev polynomials.
Then the residual polynomial $P_{2t}$ of even diploma related to this methodology
will be written when it comes to Chebyshev polynomials of the primary ($T_{t}$) and second form $(U_{t})$
as
start{align}label{eq:theoremP2t}
P_{2t}(lambda) &= mother^t left( tfrac{2 mother}{1 + mother},
T_{2t}(zeta(lambda))
+ tfrac{1 – mother}{1 + mother} , U_{2t}(zeta(lambda))proper),,
finish{align}
with $zeta(lambda) = frac{1+mother}{2 sqrt{mother}}sqrt{(1 – tfrac{stepzero}{1 + mother}lambda)(1 – tfrac{stepone}{1+mother} lambda) }$.
We are going to show this by induction. We are going to use that Chebyshev polynomials of the primary form $T_t$ and of the second form $U_t$ observe the recurrence
start{align}
&T_{2t + 2}(lambda) = (4 lambda^2 – 2) T_{2t}(lambda) – T_{2n – 2}(lambda) label{eq:recursion_first_kind}
&U_{2t + 2}(lambda) = (4 lambda^2 – 2) U_{2t}(lambda) – U_{2n – 2}(lambda) label{eq:recursion_second_kind},,
finish{align}
with preliminary situations $T_{0}(lambda) = 1,,~T_2(lambda) = 2 lambda^2 – 1$ and $U_{0}(lambda) = 1,,~U_2(lambda) = 4 lambda^2 – 1$.
Let $widetilde{P}_t$ be the right-hand facet of eqref{eq:theoremP2t}.
We begin with the case $t=0$ and $t=1$. From the preliminary situations of Chebyshev polynomials we see that
start{align}
widetilde{P}_0(lambda) &= smalldfrac{2mom}{1 + mother}
+ smalldfrac{1 – mother}{1 + mother} = 1 = P_0(lambda)
widetilde{P}_2(lambda) &= mother left( {smalldfrac{2mom}{1 + mother}}
(2 zeta(lambda)^2 – 1)
+ {smalldfrac{1 – mother}{1 + mother}} (4 zeta(lambda)^2 – 1)proper)
&= mother left( dfrac{4}{1 + mother}zeta(lambda)^2 – 1 proper)
&= 1 – (stepzero + stepone)lambda +{smalldfrac{stepzero stepone }{1+mother}}lambda^2 ,.
finish{align}
Let’s now compute $P_2$ from its recursive system eqref{eq:residual_cyclical_recurrence}, which provides:
start{align}
{P}_2(lambda) &= (1 + mother – stepone lambda)P_1(lambda) – mother P_0(lambda)
&= (1 + mother – stepone lambda)(1 – {smalldfrac{stepzero lambda}{1 + mother}}) – mother
&= 1 – (stepzero + stepone)lambda +{smalldfrac{stepzero stepone }{1+mother}}lambda^2 ,.
finish{align}
and so we will conclude that $widetilde{P}_2 = P_2$.
Now lets assume it is true as much as $t$. For $t+1$ now we have by the recursive system eqref{eq:recursive_formula}
start{align}
P_{2t+2}(lambda) &overset{textual content{Eq. eqref{eq:recursive_formula}}}{=} && left( 4 mother zeta(lambda)^2 – 2 mother proper) P_{2t}(lambda) – mother^2 P_{2t – 2}(lambda)
&overset{textual content{induction}}{=} && mother^{t+1}left( 4 zeta(lambda)^2 – 2 proper) left( {smalldfrac{2 mother}{mother+1}}, T_{2t}(zeta(lambda))
+ {smalldfrac{1 – mother}{1 + mother}}, U_{2t}(zeta(lambda))proper)
& &-& mother^{t+1} left( {smallfrac{2 mother}{mother+1}},
T_{2(t-1)}(zeta(lambda))
+ {smallfrac{1 – mother}{1 + mother}}, U_{2(t-1)}(zeta(lambda))proper)
&overset{textual content{Eq. (ref{eq:recursion_first_kind}, ref{eq:recursion_second_kind}})}{=} && mother^{t+1}left( {smallfrac{2 mother}{mother+1}}, T_{2(t+1)}(zeta(lambda)) + {smallfrac{1 – mother}{1 +
mother}}, U_{2(t+1)}(zeta(lambda))proper)
finish{align}
the place within the second id we used the induction speculation and within the third one the recurrence of even Chebyshev
polynomials.
This concludes the proof.
It is All In regards to the Hyperlink Operate
Partially 2 of this sequence of weblog posts, we derived the residual polynomial $P^{textual content{HB}}_{2t}$ of (fixed step-size) heavy ball. We expressed this polynomial when it comes to Chebyshev polynomials as
start{equation}
P^{textual content{HB}}_{2t}(lambda) = {coloration{colormomentum}m}^{t} left( {smallfrac{2
{coloration{colormomentum}m}}{1 + {coloration{colormomentum}m}}},
T_{2t}(sigma(lambda))
+ {smallfrac{1 – {coloration{colormomentum}m}}{1 + {coloration{colormomentum}m}}},
U_{2t}(sigma(lambda))proper),.
finish{equation}
with $sigma(lambda) defas {smalldfrac{1}{2sqrt{{coloration{colormomentum}m}}}}(1 +
{coloration{colormomentum}m} –
{coloration{colorstepsize} h},lambda)$.
It seems that the above is basically the identical polynomial because the one related to the cyclical heavy ball within the earlier theorem eqref{eq:theoremP2t}, the one distinction being the time period contained in the Chebyshev polynomials (denoted $sigma$ for the fixed step-size and $zeta$ for the cyclical step-size variant). We’ll name these hyperlink capabilities
.
Within the case of fixed step-sizes, it is a linear operate $sigma(lambda)$, whereas for the cyclical step-size system is the extra sophisticated operate $zeta(lambda)$:
start{align}
sigma(lambda) &= {smalldfrac{1}{2sqrt{{coloration{colormomentum}m}}}}(1 +
{coloration{colormomentum}m} –
{coloration{colorstepsize} h},lambda) & textual content{ (fixed step-sizes)}
zeta(lambda) &= {smalldfrac{1+mother}{2 sqrt{mother}}}sqrt{huge(1 – {smalldfrac{stepzero}{1 + mother}}lambdabig)huge(1 – {smalldfrac{stepone}{1+mother}} lambdabig) }
& textual content{(cyclical step-sizes)}
finish{align}
Understanding the variations between these two hyperlink capabilities is vital to understanding cyclical step sizes.
Whereas the hyperlink operate for the fixed step-size heavy ball is at all times real-valued, the hyperlink operate of the cyclical variant is complex-valued. Therefore, to offer a significant certain on the residual polynomial we have to perceive the behaving of Chebyshev polynomials within the complicated airplane.
The 2 faces of Chebyshev polynomials
It seems that Chebyshev polynomials at all times develop exponentially within the diploma exterior of the actual section $[-1, 1]$. In different phrases, Chebyshev polynomials have two clear-cut regimes: linearly bounded in $[-1, 1]$, and exponentially diverging exterior.

Magnitude of Chebyshev polynomials of the primary form within the complicated airplane. $x$ and $y$ coordinates characterize the (complicated) enter, magnitude of the output is displayed on the $z$ axis, whereas the argument is represented by the colour.
Zeros of Chebyshev polynomials are concentrated in the actual $[-1, 1]$ section, and the polynomials diverge exponentially quick exterior it.
The next lemma formalizes this for the convex mixture of Chebyshev polynomials $frac{2{coloration{colormomentum}m}}{1 + {coloration{colormomentum}m}}, T_{t}(z)
+ {smallfrac{1 – {coloration{colormomentum}m}}{1 + {coloration{colormomentum}m}}}, U_{t}(z)
$ that seem within the heavy ball methodology:
Let $z$ be any complicated quantity, the sequence
$
left(huge|
smallfrac{2{coloration{colormomentum}m}}{1 + {coloration{colormomentum}m}}, T_{t}(z)
+ {smallfrac{1 – {coloration{colormomentum}m}}{1 + {coloration{colormomentum}m}}}, U_{t}(z)
huge|proper)_{t geq 0}
$
grows exponentially in $t$ for $z notin [-1, 1]$, whereas in that interval they’re bounded as $|T_t(z)| leq 1, |U_t(z)| leq t+1$.
For this proof we’ll use the next specific expression for Chebyshev polynomials, legitimate for any complicated quantity $z$ apart from 1 and -1:
T_t(z) = &~ frac{xi^t + xi^{-t}}{2} nonumber
U_t(z) = &~ frac{xi^{t+1} – xi^{-(t+1)}}{xi – xi^{-1}} label{eq:t_and_u},.
finish{align}
with $xi defas z + sqrt{z^2 – 1}$, which means $xi^{-1} = z – sqrt{z^2 – 1}$.
start{equation}label{eq:chebyshevs_xi}
smallfrac{2{coloration{colormomentum}m}}{1 + {coloration{colormomentum}m}}, T_{t}(z)
+ {smallfrac{1 – {coloration{colormomentum}m}}{1 + {coloration{colormomentum}m}}}, U_{t}(z)
=
frac{(xi^2 – mother)xi^t + (mother xi^2 – 1)xi^{-t}}{(1+mother)(xi^2-1)},.
finish{equation}
This expression has 2 exponential phrases. Relying on the magnitude of $xi$, now we have the next conduct:
- If $|xi|gt 1$, then the primary time period grows exponentially quick.
- If $|xi|lt 1$, then the second time period grows exponentially quick.
- If $|xi|=1, |xi| neq pm 1$, then the sequence of curiosity is bounded.
Due to this fact,
$
left(huge|
smallfrac{2{coloration{colormomentum}m}}{1 + {coloration{colormomentum}m}}, T_{t}(z)
+ {smallfrac{1 – {coloration{colormomentum}m}}{1 + {coloration{colormomentum}m}}}, U_{t}(z)
huge|proper)_{t geq 0}
$
is bounded solely when $|xi|=1$ and grows exponentially quick in any other case. We’re nonetheless left with the duty of discovering the complicated numbers $z$ for which $xi$ has unit modulus.
For this, word that when $xi$ has a modulus 1, then its inverse $z – sqrt{z^2 – 1}$ can be its complicated conjugate.
This suggests that the actual a part of $xi$ and $xi^{-1}$ coincide, and so $sqrt{z^2 – 1}$ is solely imaginary and $z in (-1, 1)$.
Lastly, for the case $z in { -1, +1}$ which we excluded at the start of the proof, we will use the identified bounds $|T_t(pm 1)| leq 1$, $|U_t(pm 1)| leq (t+1)$ to conclude that it doesn’t develop exponentially.
A more in-depth look into the hyperlink operate
Given the earlier lemma that exhibits that our mixture of Chebyshev polynomials grows exponentially within the diploma exterior of $[-1, 1]$, we search to grasp when the picture of the hyperlink operate lies on this interval
because it’s on this regime the place we’ll count on to realize the very best charges. We’ll name the set of parameters that confirm this situation the sturdy area.
The hyperlink operate $sigma$ for the fixed ste-size heavy ball is a linear operate, so its preimage $sigma^{-1}([- 1, 1])$ can be an interval. This explains why most analyses of the heavy ball assume the eigenvalues belonging to a single interval.

Whereas the preimage $sigma^{-1}([-1, 1])$ related to the fixed step-size hyperlink operate is at all times an interval,
issues turn out to be extra fascinating for the cyclical hyperlink operate $zeta$. On this case, the preimage will not be at all times an interval:
The preimage $zeta^{-1}([-1, 1])$ of the cyclical step-size hyperlink operate is a union of two disjoint intervals. $zeta(lambda)$ is bigger than 1 to the left of the left interval
and smaller than -1 to the best of the best interval. In between each intervals,
$zeta(lambda)$ is solely imaginary.
For visualization functions, we select the department of the sq. root that agrees in signal with $(1 + mother – stepone lambda)$. This does not have an effect on the speed, since this time period solely seems squared within the residual polynomial expression.

The preimage $zeta^{-1}([-1, 1])$ related to the cyclical step-size hyperlink operate is at all times a union of two intervals.
Chihara
Theodore Seio Chihara is thought for his analysis within the subject of orthogonal polynomials and
particular capabilities. He wrote the very influential e-book An Introduction to Orthogonal Polynomials.
The household of Al-Salam-Chihara and Brenke-Chihara polynomials are named in his honor.
start{equation}
start{aligned}
zeta^{-1}([-1, 1]) = & left[frac{(1+mom)(stepzero + stepone)-Delta}{2 stepzero stepone}, frac{1+mom}{stepone}right]
& bigcup left[frac{1+mom}{stepzero}, frac{(1+mom)(stepzero + stepone)+Delta}{2 stepzero stepone}right],,
finish{aligned}label{eq:preimage}
finish{equation}
with $Delta defas sqrt{(1+mother)^2 (stepzero + stepone)^2- 4 (1 – mother)^2 stepzero stepone}$.

One of many primary variations between polynomials with fixed and cyclical coefficients is the conduct of their zeros. Whereas the zeros of orthogonal polynomials with fixed coefficients focus in an interval, these of orthogonal polynomials with various coefficients focus as an alternative on a union of two disjoint intervals.
This end result has profound implications. First, keep in mind that due to the exponential divergence of Chebyshev polynomials exterior the $[-1, 1]$ interval, we might just like the picture of the Hessian eigenvalues to be on this $[-1, 1]$ interval. The earlier end result says that the eigenvalue help set that may assure that is not a single interval (as was the case for the fixed step-size heavy ball) however a union of two disjoint intervals. We’ll discover the implications of this mannequin within the subsequent part.
A Refined Mannequin of the Eigenvalue Help Set
Within the following we’ll assume that the eigenvalues of $HH$ lie in a set $Lambda$ that could be a union of two intervals of equal dimension:
start{align}
Lambda defas [muone, Lone] cup [mutwo, Ltwo],,
finish{align}
with $Lone – muone = Ltwo – mutwo$. Observe that this parametrization is strictly extra common than the classical assumption that the eigenvalues lie inside an interval since we will at all times take $Lone = mutwo$, wherein case $Lambda$ turns into the $[muone, Ltwo]$ interval.
A amount that can be essential afterward is the relative hole or eigengap:
start{equation}
R defas frac{mutwo – Lone}{Ltwo – muone},.
finish{equation}
This amount measures the dimensions of the hole between the 2 intervals. $R=0$ implies that the 2 intervals are adjoining ($Lone = mutwo$ and the set $Lambda$ is in follow a single interval), whereas $R=1$ implies as an alternative that every one eigenvalues are concentrated across the largest and smallest worth.
It seems that many deep neural networks Hessians match into this mannequin with a non-trivial hole.
Hessian eigenvalue histogram for a quadratic
goal on MNIST. The outlier eigenvalue at $Ltwo$ generates a non-zero relative hole R = 0.77. On this case,
the 2-cycle heavy ball methodology has a sooner asymptotic
fee than the single-cycle one (see Part 3.2)

Extra complicated eigenvalue constructions are equally potential to mannequin with longer cycle lengths. Whereas we cannot go into these strategies on this weblog put up, some are mentioned in the paper.
A Rising Strong Area
The set of parameters for which the picture of the hyperlink operate is within the $[-1, 1]$ interval known as the sturdy area.
start{equation}
r_{2t} defas max_{lambda in Lambda}|P_{2t}(lambda)| leq mother^{t} left( 1
+ {smallfrac{1 – {coloration{colormomentum}m}}{1 + {coloration{colormomentum}m}}}, 2 tright),.
finish{equation}
Asymptotically, the primary exponential time period $mother^{t}$ dominates, and now we have the asymptotic fee
start{equation}label{eq:asymptotic_rate}
limsup_{t to infty} sqrt[2t]{r_{2t}} = sqrt{mother}
finish{equation}
Surprisingly, this $sqrt{mother}$ asymptotic fee is the identical expression for fixed step-size heavy ball!. It may appear we have performed all this work for nothing …
Luckily, this isn’t true, our work has not been in useless.
There is a speedup, however the reason being delicate. Whereas it is true that the expression for the convergence fee is identical for fixed step-size and cyclical, the sturdy area will not be the identical. Therefore, the minimal momentum that we will plug on this expression will not be the identical, probably leading to a special asymptotic fee.
We now search to seek out the smallest momentum parameter we will take whereas staying throughout the sturdy area, which is to say whereas the pre-image $zeta^{-1}([-1, 1])$ comprises the eigenvalue set $Lambda$.
The world of that pre-image will be computed from the system eqref{eq:preimage}, and it seems that this space elements as a product of two phrases which can be growing in $mother$:
start{align}
& frac{sqrt{(1+mother)^2 (stepone+stepzero)^2- 4 (1 – mother)^2 stepzero stepone}}{stepzero stepone} + (1+mother)(frac{1}{stepone} – frac{1}{stepzero})
&= underbrace{vphantom{left[ sqrt{(stepone + stepzero)^2 – 4 left(frac{1-mom}{1+mom}right)^2} + stepzero – stepone right]}left[frac{1 + mom}{stepzero stepone} right]}_{textual content{constructive growing}}underbrace{left[ sqrt{(stepone + stepzero)^2 – 4 left(frac{1-mom}{1+mom}right)^2} + stepzero – stepone right]}_{textual content{constructive growing}},.
finish{align}
start{equation}
start{aligned}
zeta(muone) = 1,,quad
zeta(Lone) = 0 ,,quad
zeta(mutwo) = 0 ,,quad
zeta(Ltwo) = -1 ,.
finish{aligned}
finish{equation}
From the second and third we get the optimum step-size parameters
start{equation}
stepzero = frac{1+mother}{mutwo}~,quad stepone = frac{1+mother}{Lone},.
finish{equation}
The worth of those optimum step-sizes is illustrated within the determine under, the place we will see

Convergence fee (in coloration) for each alternative of step-size parameters. The optimum step-sizes are highlighted in orange.
We will see how the optimum step-sizes are equivalent for a trivial eigengap $(R=0)$, and develop additional aside with $R$.
Changing into the primary equation (or fourth, they’re redundant)
and transferring all momentum phrases to 1 facet now we have
start{align}
huge({smalldfrac{1 + mother}{2 sqrt{mother}}}huge)^2
& = {smalldfrac{Lone mutwo}{(Lone – muone)(mutwo – muone)}},.
finish{align}
Let $rho defas frac{Ltwo+muone}{Ltwo-muone} = frac{1 + kappa}{1-kappa}$ be the inverse of the linear convergence fee of the Gradient Descent methodology.
With this notation, we will rewrite the above equation as
start{equation}
Massive({smalldfrac{1 + mother}{2 sqrt{mother}}}Massive)^2 = frac{rho^2 – R^2}{1 – R^2},.
finish{equation}
Fixing for $mother$ lastly offers
start{equation}
mother = Massive( frac{sqrt{rho^2 – R^2} – sqrt{rho^2 – 1}}{sqrt{1 – R^2}}Massive)^2,.
finish{equation}
With these parameters, we will now write the cyclical heavy ball methodology with optimum parameters. It is a methodology that requires information of the smallest and largest Hessian eigenvalue and the relative hole $R$:
Cyclical Heavy Ball with optimum parameters
Enter: beginning guess $xx_0$ and eigenvalue bounds $muone, Lone, mutwo, Ltwo$.
Set: $rho = frac{Ltwo+muone}{Ltwo-muone}$, $R=frac{mutwo – Lone}{Ltwo – muone}$,
$mother = huge( frac{sqrt{rho^2 – R^2} – sqrt{rho^2 – 1}}{sqrt{1 – R^2}}huge)^2$
$xx_1 = xx_0 – frac{1}{mutwo} nabla f(xx_0)$
For $t=1, 2, ldots$
start{align*}label{eq:momentum_update_optimal}
&textual content{${coloration{colorstepsize}h_t} = textstylefrac{1+mother}{mutwo}$ if $t$ is even and ${coloration{colorstepsize}h_t} = textstylefrac{1+mother}{Lone}$ in any other case}
&xx_{t+1} = xx_t – {coloration{colorstepsize}h_t} nabla
f(xx_t)+ {coloration{colormomentum} m}(xx_{t} – xx_{t-1})
finish{align*}
Convergence Charges
We have seen within the earlier part that within the sturdy area, the convergence fee is a straightforward operate of the momentum parameter. The one factor left to do is then to plug our optimum parameter into this system eqref{eq:asymptotic_rate}. The next corollary gives it and an asymptotic model.
Let $x_t$ be the iterate generated by the above algorithm after a good variety of steps $t$ and let $rho defas frac{Ltwo+muone}{Ltwo-muone} = frac{1 + kappa}{1-kappa}$ be the inverse of the linear convergence fee of the Gradient Descent methodology. Then we will certain the iterate suboptimality by a product of two phrases, the primary of which decreases exponentially quick, whereas the second will increase linearly in $t$:
start{equation}
fracx_0 – x_star leq underbrace{vphantom{sum_i}textstyleBig(frac{sqrt{rho^2 – R^2} – sqrt{rho^2 – 1}}{sqrt{1 – R^2}}Massive)^{t} }_{textual content{exponential lower}} , underbrace{Massive( 1 + tsqrt{smalldfrac{rho^2-1}{rho^2 – R^2}}Massive)}_{textual content{linear improve}},.
finish{equation}
Asymptotically, the exponential time period dominates, and now we have the next asymptotic fee issue:
start{equation}
label{eq:cyclic_rate}
limsup_{t to infty} sqrt[2t]{frac{|x_{2t} – x_star|}x_0 – x_star} leq frac{sqrt{rho^2 – R^2} – sqrt{rho^2 – 1}}{sqrt{1 – R^2}},.
finish{equation}
How do these examine with these of the fixed step-size heavy ball methodology with optimum parameters (Polyak heavy ball)?
The asymptotic fee of Polyak heavy ball is $r^{textual content{PHB}} defas rho – sqrt{rho^2 – 1}$, and so we might like to check
start{equation}label{eq:polyak_rate}
start{aligned}
&r^{textual content{CHB}} = frac{sqrt{rho^2 – R^2} – sqrt{rho^2 – 1}}{sqrt{1 – R^2}}
textual content{vs } &r^{textual content{PHB}} defas rho – sqrt{rho^2 – 1},.
finish{aligned}
finish{equation}
The very first thing we will say is that each coincide when $R=0$, and that $r^{textual content{CHB}}$ is a lowering operate of $R$, so the speed improves with the relative hole. Aside from that, it is not clear the way to summarize the development by an easier system.
On the ill-conditioned regime, the place the inverse situation quantity goes to zero ($kappa defas tfrac{mu}{L} to 0$), which can be the primary case of curiosity, we’ll be capable to present an approximation that sheds some mild. On this regime, now we have the next charges (decrease is healthier):
&r^{textual content{PHB}} underset{kappa rightarrow 0}{=} 1 – 2sqrt{kappa} + o(sqrt{kappa})
&r^{textual content{CHB}} underset{kappa rightarrow 0}{=} 1 – 2frac{sqrt{kappa}}{{coloration{purple}sqrt{1-R^2}}} + o(sqrt{kappa}),,label{eq:approx}
finish{align}
the place $o(sqrt{kappa})$ comprises which to go zero sooner than $sqrt{kappa}$ as $kappa rightarrow 0$.
This sheds some mild on the development: the cyclical scheduler permits us to divide the complexity of the strategy by an element of $frac{1}{coloration{purple}sqrt{1-R^2}},$!
The determine under compares the convergence fee of Polyak heavy ball (Polyak), the cyclical heavy ball (Cyclical) and its approximated fee eqref{eq:approx} (Approx, in dashed strains). We see Cyclical behaving like Polyak for well-conditioned issues (small $kappa$) after which
becoming extra the super-accelerated fee (Approx) for ill-conditioned issues. This plot additionally exhibits that the approximated fee is an excellent approximation for $kappa lt 0.001$.
Convergence fee comparability between Polyak heavy ball, Cyclical heavy ball, and its approximate convergence fee.
We will see how the approximated fee gives a superb match within the ill-conditioned regime.

Conclusion and Views
On this put up, we have proven that cyclical studying charges present an efficient and sensible method to leverage a niche or bi-modal construction within the Hessian’s eigenvalues. We have additionally derived optimum parameters and proven that within the ill-conditioned regime, this methodology achieves an additional fee issue enchancment of $frac{1}{coloration{purple}sqrt{1-R^2}}$ over the accelerated fee of Polyak heavy ball, the place $R$ is the relative hole within the Hessian eigenvalues.
The mixture of a structured Hessian, momentum and cyclical studying charges is immensely highly effective, and right here we’re solely scratching the floor of what is potential.
Many essential circumstances haven’t but been studied, such because the non-quadratic setting (strongly convex, convex, and non-convex). Within the paper now we have empirical outcomes logistic regression displaying speedup of the cyclical heavy ball methodology, however no proof past native convergence. Equally open is the extension to stochastic algorithms.
Citing
If you happen to discover this weblog put up helpful, please think about citing as
Cyclical Step-sizes, Baptiste Goujaud and Fabian Pedregosa, 2022
with bibtex entry:
@misc{goujaud2022cyclical,
title={Cyclical Step-sizes},
creator={Goujaud, Baptiste and Pedregosa, Fabian},
url = {http://fa.bianp.internet/weblog/2022/cyclical/},
12 months={2022}
}
To quote its accompanying full-length paper, please use:
Tremendous-Acceleration with Cyclical Step-sizes, Baptiste Goujaud, Damien Scieur, Aymeric Dieuleveut, Adrien Taylor, Fabian Pedregosa. Proceedings of The twenty fifth Worldwide Convention on Synthetic Intelligence and Statistics, 2022
Bibtex entry:
@inproceedings{goujaud2022super,
title={Tremendous-Acceleration with Cyclical Step-sizes},
creator={Goujaud, Baptiste and Scieur, Damien and Dieuleveut, Aymeric and Taylor,
Adrien and Pedregosa, Fabian},
booktitle = {Proceedings of The twenty fifth Worldwide Convention on Synthetic
Intelligence and Statistics},
sequence = {Proceedings of Machine Studying Analysis},
12 months={2022}
}


