Brett‘s Choose this week is Ellipse Detection Utilizing 1D Hough Rework, by Martin Simonovsky.
Contents
Introduction
I’ve written a number of instances up to now about detecting circles in photographs (right here, right here, and right here). I’ve written, too, on drawing ellipses. At this time, I wish to write about detecting ellipses.
Since ellipses are described by extra parameters than are traces or circles, detecting ellipses is more difficult than is detecting traces or circles. And whereas we now have good performance for detecting the easier shapes (houghlines, imfindcircles), we don’t (at the moment) have a operate to detect ellipses. Enter Martin’s ellipse-detection operate.
The Supply
Luckily, and appropriately, Martin cited the supply for his algorithm; he used a paper (Y. Xie, Q. Ji. “A New Environment friendly Ellipse Detection Technique.” 1051-4651/02 IEEE, 2002) that I’ve had on my desk for fairly a while, considering that I might at some point sit all the way down to implement it in MATLAB code. I like that Martin did that work for me–it makes me recognize the File Trade all of the extra.
The Implementation
After taking part in round with Martin’s ellipseDetection() for many of a day, I’ve some ideas to share. First, acknowledge that ellipse detection is an costly reminiscence hog; the computation scales with the sq. of the variety of nonzero pixels, N, in your search picture. You will virtually actually wish to function on an “edge picture” slightly than a easy binary masks of your areas of curiosity, and to play with the operate’s 9 enter parameters to restrict the search. Amongst these parameters, you possibly can specify the vary of main axes lengths to think about, and the minimal side ratio. You may additionally specify some parameters for limiting the angles of the ellipses you search; this might be very helpful if you realize the ellipse orientations a priori. Even after such limits are used, an exhaustive search examines N x N candidates for main axes. Martin’s operate offers a parameter that permits you to commerce off between pace and accuracy. (The “randomize” parameter shouldn’t be a Boolean variable, because the identify suggests; slightly it reduces the search house from N x N to N x randomize. If randomize is 0, then the search is exhaustive–increased accuracy at a computational value.)
A Check Drive
So let’s strive it out on a pattern picture of our creation. We are able to begin with a picture containing circles, and warp it to generate ellipses:
inputImage = imread('coloredChips.png'); tform = affine2d([1 0 0; 0.75 1 0; 0 0 1]); inputImage = imwarp(inputImage, tform); imshow(inputImage) title("Check Picture")

Segmentation
I segmented the picture by:
- Utilizing the colorThresholder to create a masks of the background
- Splitting the colour picture into R, G, and B elements (imsplit)
- Masking the R, G, and B planes individually (R(backgroundMask) = 0, …)
- Re-compositing the masked planes into an RGB picture (cat)
- Changing the masked RGB picture to grayscale (im2gray)
- Calculating (with rigorously chosen enter parameters) the perimeters of the grayscale picture (edge)
- Filtering the outcomes to pick out the specified Main Axes Lengths and Areas (imageRegionAnalyzer, bwpropfilt)
In only a few minutes, I had an edge picture wherein to detect these ellipses:

Detecting the Ellipses
With this binary edge masks in hand, I used to be able to seek for ellipses–first, naively:
bestFits = ellipseDetection(edgeMask);
The operation accomplished in (simply) lower than a second, however the outcomes have been underwhelming:
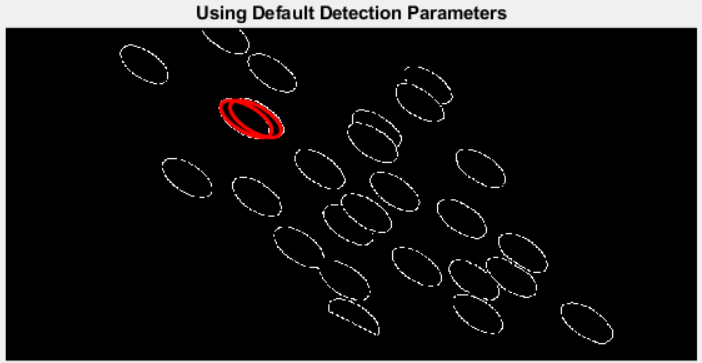
(By the best way, calling ellipseDetection() on the binary masks of the warped chips with out first calculating the perimeters took upwards of 20 minutes, and the outcomes have been even worse!)
Enhancing the Outcomes
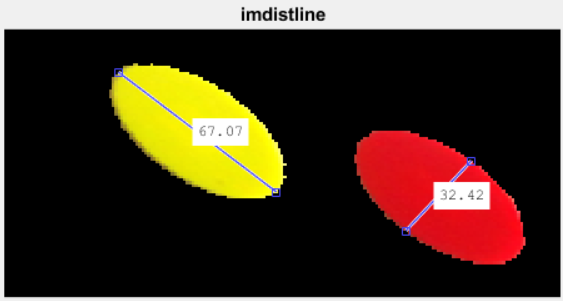
To enhance the efficiency, I judiciously chosen enter parameters to cut back the computational value. First, I used imdistline to measure the most important and minor axes lengths:
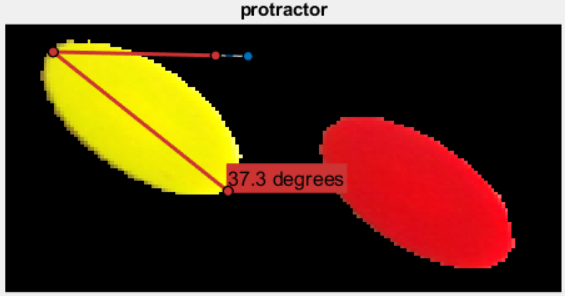
Then I used protractor to get a way of the orientations of the ellipses:
After a couple of minutes, I discovered my method to:
params.minMajorAxis = 55; params.maxMajorAxis = 75; params.minAspectRatio = 0.4; params.rotation = 35; params.rotationSpan = 10; params.randomize = 0; params.numBest = 30;
bestFits = ellipseDetection(edgeMask, params);

Paring Outcomes
Wait…what? bestFits comprises paramaters for 30 detections (a handbook rely informs me that there are 26 ellipses wholly contained within the picture), however when visualizing the outcomes, it seems that there are far fewer. What is going on on?
It seems that the algorithm is prone to reporting the identical ellipse a number of instances. (If I drag these cyan ellipses, there are different coincident ellipses beneath!)
Experimenting, I discovered it fairly helpful to dramatically overspecify the variety of ellipses I wished to detect, then to pare the ends in post-processing. Take into account:
params.smoothStddev = 0.5;
params.numBest = 1000;
bestFits = ellipseDetection(edgeMask, params);
minCenterDistance = 10;
minScore = 30;
maxAspectRatio = 0.6;
bestFits = pareEllipseFits(bestFits, ...
minCenterDistance, minScore, maxAspectRatio);
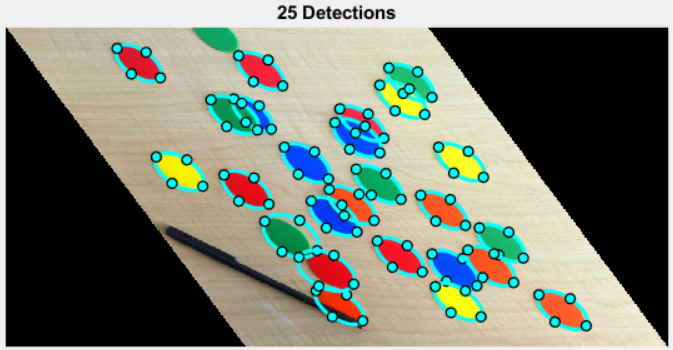
I wrote pareResults to permit filtering by minimal middle distance (to disallow overlapping detections), minimal rating, and most side ratio. Utilizing that paring strategy, I can request way more detections (params.numBest = 1000) than I really need, then discard “dangerous” outcomes. I am fairly happy with the best way it is working!
A Be aware on Visualizing the Outcomes
Lastly, I additionally wrote visualizeEllipses to name drawellipse instantly on the output of ellipseDetection.
Notes
Within the curiosity of creating this put up a bit shorter (I do know…too late!), I did not put up the entire code. If anybody want to see it, I am completely satisfied to share. Simply drop me an e mail at:
char(cumsum([98 17 -11 7 -10 7 7 -4 -47 45 -12 19 -12 15 -8 3 -7 8 -69 53 12 -2]))
Additionally, there are a number of different information on the Trade that purport to facilitate ellipse detection. Please go away me a remark if you would like to see these thought of these in a subsequent put up!
A Couple of Options
Martin’s implementation makes use of Gaussian filtering by way of fspecial. That syntax is not beneficial; the newer imgaussfilt is extra environment friendly. Additionally, the decision to fspecial requires an integer argument for the second ('hsize') parameter. (I added a name to spherical() in my model.) Lastly, since getting good outcomes requires tuning various parameters, this operate is simply begging for a code-generating app to entrance it; that is maybe a undertaking for an additional day!
Thanks, Martin…discovering this operate, and determining learn how to use it, offers me a beneficial software in my picture processing arsenal.
As at all times, I welcome your ideas and feedback.
Revealed with MATLAB® R2022a

