Simulate the Monty Corridor downside in Python 🐐🚘🐐

There is a traditional likelihood puzzle primarily based on the TV sport present “Let’s Make a Deal” and named after its host, Monty Corridor. This is the puzzle:

You’re a contestant on a sport present. In entrance of you might be three closed doorways. Behind one of many doorways is a automotive, and behind the opposite two doorways are goats. Your purpose is to select the door with the automotive.

The host asks you to decide on a door. You inform the host your selection. As an alternative of telling you whether or not your selection was appropriate, the host (who is aware of which door accommodates the automotive) opens one of many two doorways you did not select and divulges a goat.

You now have the chance to maintain your unique selection or swap your option to the door that’s nonetheless closed. Which do you have to select?

For instance, let’s fake that you just began by selecting door #1. The host opens door #3 to disclose that it accommodates a goat. Do you have to hold your unique selection of door #1 or swap your option to door #2?

Use simulations for problem-solving

One of many “superpowers” of having the ability to write code is that you should use simulations to be able to clear up issues like these. Earlier than studying my answer under, I am difficult you to jot down Python code to simulate this downside!

Particularly, I would like you to simulate that you’re a contestant on this present 1000 instances. Every time, you decide a random door as your first selection, let the host open a door that reveals a goat, after which swap your option to the door that the host did not open. With that technique (often known as the “all the time swap” technique), how typically do you win the automotive?

Listed below are a couple of particulars that I need to be clear about:

• Earlier than beginning every sport, the host randomly selects which door accommodates the automotive.
• After you make your preliminary selection, the host all the time opens one door that accommodates a goat, and it’ll all the time be a door that you just didn’t initially select. (If the host has two choices for which door to open to disclose a goat, he’ll randomly choose which of these two doorways to open.)
• After the host opens a door that accommodates a goat, you’ll all the time be given the choice to change your option to the door that’s nonetheless closed, and you’ll all the time settle for that choice.

The perfect simulation code is concise, easy-to-read, and represents the info in a chic method. Be at liberty to share your code with me within the feedback part on the backside! 👇

Under you may discover my answer, in addition to some wonderful options submitted by readers of my e-newsletter!

My answer code

I will clarify this code piece-by-piece:

Since we have to simulate random alternatives, the same old selection is Python’s random module.

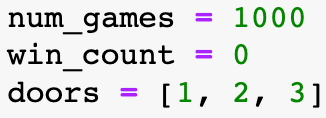
I set the variety of video games to simulate, a counter to trace the variety of wins, and a listing to characterize the three doorways.

This loop simulates 1000 impartial video games.

Throughout every sport, the host randomly selects one of many three doorways for the automotive, and the participant randomly selects one of many three doorways as their first decide for the place the automotive is likely to be. To do that, the random.selection() operate selects one of many three components from the doorways checklist.

The host should open one of many closed doorways, and I have to ensure that they are not opening the door with the automotive or the door that the participant already selected.

To do that, I convert the doorways checklist to a set, convert the automotive’s location and the participant’s first decide to a different set, after which take the distinction. Thus, host_can_open is a set of all the doorways that do not include the automotive and weren’t picked by the participant.

host_can_open accommodates both one or two doorways, and I exploit random.selection() to choose which door the host truly opens and retailer that in host_opens. (Observe: random.selection() does not work with units, which is why I transformed it to a listing.)

Subsequent, we’d like the participant to swap their decide to the one door that’s nonetheless closed. Once more, we use a set distinction operation. However why is the min() operate there?

Nicely, the set distinction operation returns a set that accommodates a single integer, equivalent to {3}. With the intention to entry simply the integer, probably the most elegant answer is to take the min (or max) of that set!

Lastly, I examine whether or not the participant’s second decide matches the situation of the automotive. In that case, we increment the variety of wins.

That is only a little bit of debugging code. It runs throughout the first 5 video games, and reveals me the worth of 4 of the objects. This permits me to double-check that the values being chosen obey the foundations of the sport.

These are known as “self-documenting expressions”, which had been added in Python 3.8. Due to the equals signal, the f-string will print first_pick=2 (for instance). With out the equals signal, the f-string would simply print 2, and I would have to recollect what every quantity represents.

Lastly, we print the win share, which is calculated by dividing the variety of wins by the variety of video games.

I begin the f-string with a n to be able to add a line break, and I add the :.1% on the finish to format the end result as a share with 1 digit after the decimal.

How typically does the participant win the automotive?

This is an instance of the output of my code:

To be clear, the primary 5 strains characterize the primary 5 video games (out of 1000). In these 5 video games, the participant gained the automotive 3 times.

The win share is how typically the participant gained the automotive through the use of the “all the time swap” technique throughout 1000 video games. On this case it was 68.8%, however you may discover that this share hovers round 66.6%. If you wish to affirm this for your self, you may run my code on-line.

This result’s counter-intuitive to many individuals (together with mathematicians and Nobel Prize winners!), however the “all the time swap” technique is twice as prone to win because the “by no means swap” technique! (To be clear, this end result solely holds if we observe all the guidelines I specified at first of this publish.)

If you wish to learn extra about this puzzle, try the prolonged Wikipedia article concerning the Monty Corridor downside.

Reader-submitted options

Certainly one of my favourite options was from Fábio C., who obtained assist from Bing AI when scripting this code:

This is what I like about Fábio’s code:

• To pick out which door the host opens, he makes use of some time loop that generates a random integer till it does not match the situation of the automotive or the participant’s first decide. Sensible!
• To pick out which door the participant adjustments to, he subtracts the participant’s first decide and the door the host opens from 6. Why? As a result of these three values (1, 2, and three) should add as much as 6!

One other answer I actually loved was from Aaron S.:

This is what I like about Aaron’s code:

• He makes use of a listing of emoji (that are legitimate characters) to characterize the prizes, after which makes use of random.shuffle() to shuffle their places.
• To pick out which door the host opens, he makes use of a intelligent checklist comprehension that zips collectively the doorways and prizes and checks for 2 situations.
• To depend the variety of wins, he runs the operate 1000 instances utilizing a generator expression after which sums the outcomes. (This works as a result of his operate returns False for a loss and True for a win, and these get transformed to 0’s and 1’s by the sum() operate.)

José P. carried out an growing variety of simulations to display that because the variety of video games will increase, the end result converges in the direction of a successful share of 66.6%:

Lastly, Conor G. despatched me a hyperlink to his assortment of Monty Corridor simulations written in Lua, Perl, C, Fortran, COBOL, Pascal, PHP, and (after all) Python!

Thanks a lot to everybody who submitted an answer! Subscribe to my weekly e-newsletter to take part in future code challenges like this! 💌

Wish to submit your code?

If you wish to share your simulation code with me, please publish a hyperlink within the feedback part under!

Listed below are two easy methods to publish your code on-line:

1. Copy and paste your code right into a GitHub Gist after which share its URL under. (Learn this publish for a fast introduction to Gists.)
2. Run your code in a Colab pocket book after which share its URL under. Nonetheless, you should click on the “Share” button and alter the “Common entry” to “Anybody with the hyperlink”.

I look ahead to seeing your code! 👩‍💻