- How exhausting is it to unravel a Rubik’s Dice?
- When are you able to say that your Rubik’s Dice is totally scrambled?
- Why would possibly the reply rely upon the place you went to highschool?
- What attention-grabbing mathematical questions are concerned?
Contents
Metrics
The issue of fixing any configuration of a Rubik’s Dice is the smallest variety of strikes required to return to the intial configuration the place every face is exhibiting a single shade.
However what, precisely, is a transfer? The so-called quarter-turn metric says a transfer is popping any face by 90 levels. The half-turn metric says turning any face by both 90 or 180 levels is a single transfer. For instance, utilizing Singmaster notation and the quarter-turn metric, the sequence “L L”, which turns the left face twice in the identical path, is 2 strikes. However within the half-move metric, the sequence turns into “L2” and counts as a single transfer.
Tomas Rokicki, who describes himself as a programmer from Palo Alto, offers some historical past at cube20.org.
Within the early days of dice arithmetic, two camps emerged on find out how to
measure the problem of a place. West coast and Stanford
mathematicians, free thinkers all, tended to choose the half-turn
metric, the place any twist of any face, whether or not 90 levels, 180 levels,
or 270 levels counted as a single transfer. The east coast crowd,
together with MIT, tended to choose the rigor of the quarter-turn metric,
the place a half-turn counted as two strikes, since in fact it may very well be
achieved by two consecutive quarter turns.
After I started improvement of a Rubik’s Dice simulator, Qube, I used to be unaware of this historical past and, despite the fact that I’m a religious West-coaster, I simply counted quarter-turns. Now a toggle swap in Qube permits use of both metric.
God’s quantity
Let Q denote a dice place,
| Q | = minimal variety of strikes to unravel Q,
Q = the set of all doable Q‘s, and
G(Q) = most over Q in Q of | Q |.
G(Q) is named “God’s quantity”. Q accommodates over 4.3*10^19 positions, so computing G(Q) is a formidable optimization downside. The definition of God’s quantity doesn’t require the optimum resolution itself, solely the variety of strikes.
Superflip
The superflip of Rubik’s dice is a configuration the place the 8 corners, the 6 face facilities, and the dice heart present the preliminary colours, however the 12 edge cubelets have the colours reversed. In 1995, Michael Reid proved that resolution of the superflip requires 20 half-turn metric strikes. In 2010, Tomas Rokicki and colleagues, utilizing lots of of computer systems at Google, carried out an enormous computation to show that no different configuration took greater than 20 strikes, cube20.org. This established that God’s quantity for the half-turn metric is
G(Q) = 20
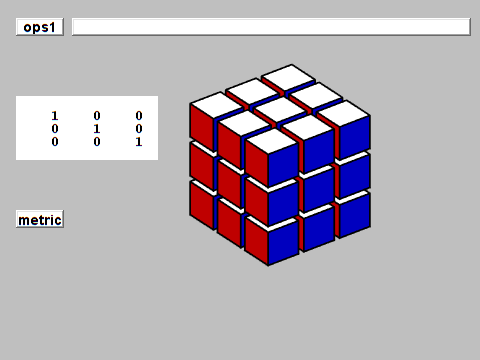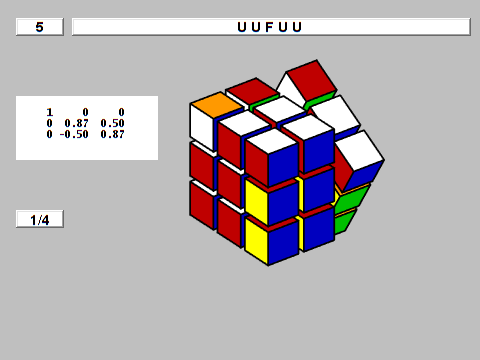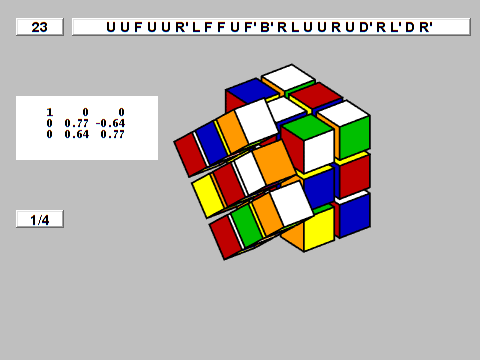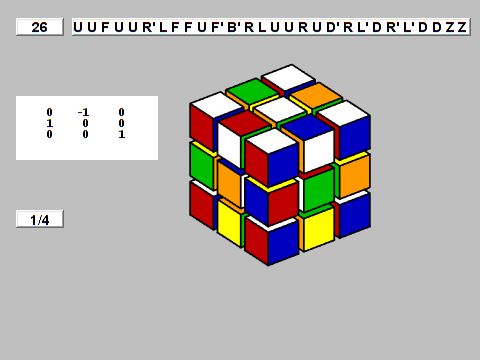
Q20
I take advantage of Q20 to indicate the superflip. Our first animation generates the superflip with 20 strikes. Just a few rotations firstly and on the finish are proven in additional element in order that we will see the rotation matrices concerned. A better decision video clip is out there at this hyperlink: Q20.mp4

The second animation exhibits an answer of Q20 in 20 strikes obtained by reversing and complementing the producing strikes. Reid’s proof exhibits that every other resolution requires a minimum of 20 strikes. The excessive decision clip is: Q20solve.mp4

There are a number of different configurations that require 20 strikes. Any configuration with G(Q) = 20 will be thought to be fully shuffled within the half-turn metric.
Q26
For the quarter-turn metric, in case you mix superflip and a configuration referred to as fourspot you could have Q26 . Solely 8 corners and two face enters are right. The sides, 4 face facilities, and the dice heart are all reversed. When 180 diploma turns are counted as two 90 diploma turns, this configuration is generated by 26 strikes and solved by reversing and complementing the 26 strikes. The excessive decision clip is: Q26.mp4
In 2014, an enormous computation on the Ohio Supercomputer Heart by Rokicki and Morley Davidson proved that solely Q26 (and its two rotations) required 26 quarter-turn strikes All different configurations want fewer. cube20.org. So, this established that God’s quantity for the half-turn metric is
G(Q) = 26
The excessive decision clip is: Q26solve.mp4

Examine
Let’s examine Q20 and Q26 by alternating between the 2.

The kind 3 nook items are the identical in Q20 and Q26, and are within the right preliminary place.

The kind 2 edge items are additionally the identical in Q20 and Q26, however are reversed from their preliminary place.

All of the motion is with cubelets of kind 0 and sort 1. In an actual, bodily Rubik’s Dice, that is one stable piece that holds the Dice collectively.
Revealed with MATLAB® R2022b


