Enter: 3
Output: 3
Clarification: There are 3 ways to climb to the highest.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step.
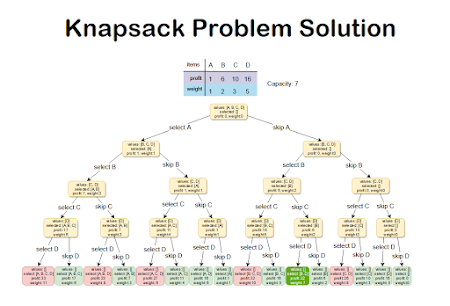
That is one other frequent Dynamic programming-based coding drawback and a sample which may resolve many such questions. In the sort of drawback, you may be given the weights and earnings of ’N’ gadgets, put this stuff in a knapsack which has a
capability ‘C’. Your purpose: get the utmost revenue from the gadgets within the knapsack. Every merchandise can solely be chosen as soon as.
Objects: { Apple, Orange, Banana, Melon }
Weight: { 2, 3, 1, 4 }
Revenue: { 4, 5, 3, 7 }
Knapsack capability: 5
Apple + Orange (whole weight 5) => 9 revenue
Apple + Banana (whole weight 3) => 7 revenue
Orange + Banana (whole weight 4) => 8 revenue
Banana + Melon (whole weight 5) => 10 revenue
3. Edit Distance Downside
This is without doubt one of the simpler dynamic programming issues. On this query, you may be given two phrases word1 and word2, to search out the minimal variety of operations required to transform word1 to word2.
You have got the next 3 operations permitted on a phrase:
- Insert a personality
- Delete a personality
- Exchange a personality
Enter: word1 = “horse”, word2 = “ros”
Output: 3
Clarification:
horse -> rorse (substitute ‘h’ with ‘r’)
rorse -> rose (take away ‘r’)
rose -> ros (take away ‘e’)
2. Longest palindromic subsequence
That is one other frequent Dynamic programming query and sample. In the sort of DP query, you may be given a sequence, discover the size of its Longest Palindromic Subsequence (or LPS). In a palindromic subsequence, parts learn the identical from side to side.
A subsequence is a sequence that may be derived from one other sequence by deleting some or no parts with out altering the order of the remaining parts.
Instance 1:
Enter:
“bbbab”
Output:
4
Clarification: LPS is “bbbb”.
4. Finest Time to Purchase and Promote Inventory
This is without doubt one of the hard Dynamic programming issues which want some expertise to unravel. On this query, you may be given an array for which the ith factor is the worth of a given inventory on day i.
If you happen to have been solely permitted to finish at most one transaction (i.e., purchase one and promote one share of the inventory), design an algorithm to search out the utmost revenue.
Notice that you simply can’t promote a inventory before you purchase one.
Instance 1:
Enter: [7,1,5,3,6,4]
Output: 5
Clarification: Purchase on day 2 (worth = 1) and promote on day 5 (worth = 6), revenue = 6-1 = 5.
Not 7-1 = 6, because the promoting worth must be bigger than shopping for worth.
You possibly can do this drawback by yourself however should you caught you can too see the answer right here on Educative.
5. The Fibonacci drawback
This is without doubt one of the best dynamic programming questions and lots of of you might have already solved it with out even understanding that you’re utilizing Dynamic programming. That is additionally the most typical instance of DP and lots of instructors use Fibonacci numbers
to show Dynamic programming. On this query, you may be requested to jot down a operate to calculate the nth Fibonacci quantity.
Fibonacci numbers are a sequence of numbers through which every quantity is the sum of the 2 previous numbers. The primary few Fibonacci numbers are 0, 1, 2, 3, 5, 8, and so forth.
We are able to outline the Fibonacci numbers as:
Fib(n) = Fib(n-1) + Fib(n-2) for n > 1
Provided that: Fib(0) = 0, and Fib(1) = 1
You too can see my answer of how one can calculate the Nth Fibonacci quantity in Java to be taught extra about how one can resolve this drawback.
6. The Coin Change Downside
You’re given cash of various denominations and a complete sum of money quantity. Write a operate to compute the fewest variety of cash that it’s worthwhile to make up that quantity. If that sum of money can’t be made up of any mixture of
the cash, return -1.
Instance 1:
Enter: cash = [1, 2, 5], quantity = 11
Output: 3
Clarification: 11 = 5 + 5 + 1
7. Longest frequent substring
Given two strings 1’ and ‘s2’, discover the size of the longest substring frequent in each the strings.
Instance 1:
Enter: s1 = “abdca”
s2 = “cbda”
Output: 2
Clarification: The longest frequent substring is “bd”.
8. Longest frequent subsequence
Given two strings 1’ and ‘s2’, discover the size of the longest subsequence which is frequent in each the strings.
Instance 1:
Enter: s1 = “abdca”
s2 = “cbda”
Output: 3
Clarification: The longest substring is “bda”.
9. Equal Subset Sum Partition Downside
That is one other common Dynamic Programming query that’s similar to the Knapsack drawback. If you understand how to unravel knapsack then you possibly can resolve this too.
In his drawback you might be given a set of constructive numbers, discover if we will partition it into two subsets such that the sum of parts in each the subsets is equal.
Instance 1:
Enter: {1, 2, 3, 4}
Output: True
Clarification: The given set might be partitioned into two subsets with equal sum: {1, 4} & {2, 3}
Instance 2:
Enter: {1, 1, 3, 4, 7}
Output: True
Clarification: The given set might be partitioned into two subsets with equal sum: {1, 3, 4} & {1, 7}
Instance 3:
Enter: {2, 3, 4, 6}
Output: False
Clarification: The given set can’t be partitioned into two subsets with an equal sum.
10. Steady Subarray Sum
That is one other common dynamic programming-based coding drawback from interviews. On this drawback, you may be given a listing of non-negative numbers and a goal integer okay, write a operate to verify if the array has a steady subarray of
dimension no less than 2 that sums as much as a a number of of okay, that’s, sums as much as n*okay the place n can be an integer.
Instance 1:
Enter: [23, 2, 4, 6, 7], okay=6
Output: True
Clarification: As a result of [2, 4] is a steady subarray of dimension 2 and sums as much as 6.
That is all about among the steadily requested Dynamic Programming issues from Interviews. Btw, that is only a small pattern of the dynamic programming ideas and issues you could encounter in a coding interview. Fixing these issues offers you sufficient thought about how one can determine Dynamic programming issues throughout coding interviews in addition to how one can resolve them in a restricted time. These questions additionally cowl all important Dynamic programming patterns just like the Knapsack drawback which can be utilized to unravel a number of DP issues.
Thanks for studying this text thus far. If you happen to like these Dynamic Programming issues and interview questions then please share them with your pals and colleagues. You probably have any questions or suggestions then please drop a word.