Gershgorin Graphics – Nick Higham

February 15, 2023

123

It’s not so typically in numerical linear algebra that the plots we produce are visually engaging. This plot got here up in some MATLAB experiments. Are you able to guess what it’s?

I plotted the Gershgorin discs of a stochastic matrix: a matrix with nonnegative components and row sums all equal to $1$ . The Gershgorin discs for an $ntimes n$ matrix $A$ are the $n$ discs within the advanced aircraft outlined by

$notag Big{ zinmathbb{C}: |z-a_{ii}| le displaystylesum_{jne i} |a_{ij}|Big}, quad i=1colon n.$

Gershgorin’s theorem says that the eigenvalues of $A$ lie within the union of the discs.

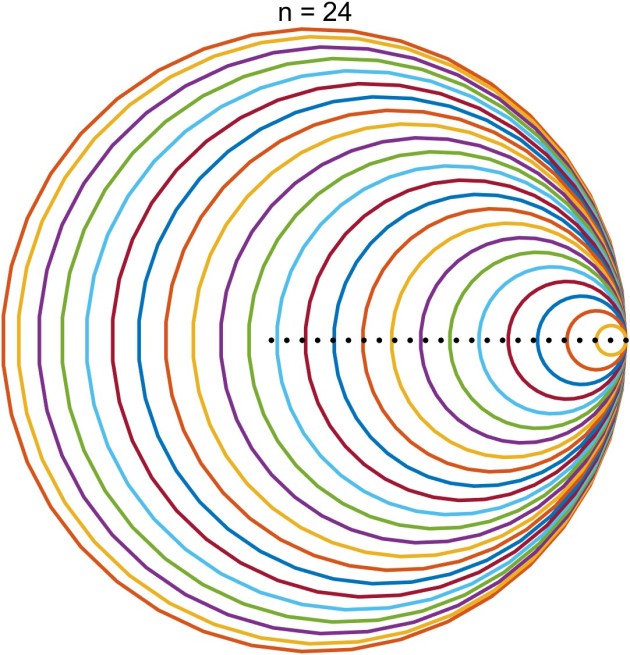
Why do the discs kind this attention-grabbing sample? For a stochastic matrix the $i$ th Gershgorin disc is

$notag Big{ zinmathbb{C}: |z - a_{ii}| le displaystylesum_{jne i} a_{ij} = 1 - a_{ii} Big}.$

This disc goes via $1$ and the nearer $a_{ii}$ is to $1$ the smaller the radius of the disc, so the discs are nested, with the disc similar to $min_i a_{ii}$ containing all of the others.

The matrix used for the plot is A = anymatrix('core/symmstoch',64) from the Anymatrix assortment. It has diagonal components roughly uniformly distributed on $[0,1]$ , so the facilities of the discs are roughly equally spaced and shrink because the facilities transfer to the precise.

The picture above is for the matrix of dimension $n = 64$ . The black dots are the eigenvalues. Right here is the plot for $n = 24$ . The perform used to supply these plots is gersh from the Matrix Computation Toolbox.