Issue: ★ ★ ★ ★
Calculating a factorial is a standard programming train, usually coupled with introducing the idea of recursion. Mathematically, the factorial has a twin: the subfactorial. Its calculation generally is a enjoyable programming problem, which is the topic of this month’s Train.
As a overview, a factorial is a worth written as n!. The worth represents integer n multiplied sequentially. For instance, 5! is 1×2×3×4×5, which equals 120. This worth is the variety of permutations potential with 5 objects.
Determine 1 illustrates 3! or three factorial. It reveals the variety of methods to rearrange three objects, which is what 3! represents.

Determine 1. The worth 3! reveals what number of methods to rearrange three objects. 3! = 6 completely different preparations.
The subfactorial works alongside comparable traces. It’s written with the exclamation level earlier than the worth: subfactorial three is !3. The subfactorial limits the preparations in order that no objects will be in the identical place as within the authentic. Worth !3 calls out all non-unique preparations for 3 objects. An instance is proven in Determine 2.

Determine 2. Three subfactorial (!3) reveals that solely two preparations are potential compared with the unique. !3 = 2.
The very best rationalization of the subfactorial course of, additionally referred to as derangement, is present in this video from Andy Math. Do take time to look at it, because it describes a method you should use to calculate subfactorials. The method is illustrated in Determine 3.
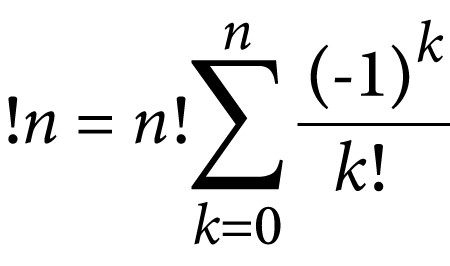
Determine 3. The equation for calculating a subfactorial.
Your process for this month’s Train is to put in writing code that outputs values for subfactorials !0 by means of !13. You need to use the equation from Determine 3 as your inspiration, which is what I did. You can too take a look at the Derangement Wikipedia web page, which affords extra formulation and mathematical mumbojumbo.
Right here is output from my resolution, the listing of subfactorial values for !0 by means of !13:
!0 = 1
!1 = 0
!2 = 1
!3 = 2
!4 = 9
!5 = 44
!6 = 265
!7 = 1854
!8 = 14833
!9 = 133496
!10 = 1334961
!11 = 14684570
!12 = 176214841
!13 = 2290792932
As with factorials, these subfactorials are recognized values, although you’ll be able to’t simply write an answer that outputs the outcomes proven above. No, it’s essential to code an answer in C.
Do this Train by yourself. I’ll publish my resolution in per week.

