Calculating the Subfactorial – Answer

Do you are feeling adequately deranged working this month’s Train? I’m extra of a math fanboy than an professional, but I loved the method of coding a subfactorial based mostly within the equation offered.

My answer does require a recursive perform to find out a factorial; factorials are wanted when calculating a subfactorial. However my derange() perform needn’t be recursive. It’s sequential, which is clear when trying on the system proven in Determine 1.

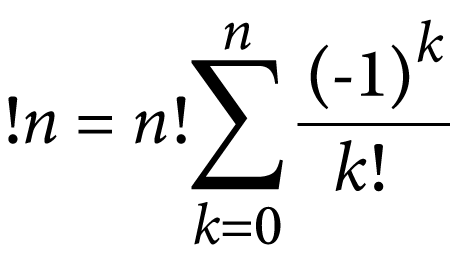
Determine 1. The equation for calculating a subfactorial.

Recursive capabilities work properly for continued fractions, however the equation in Determine 1 is finite. A loop is ample to plow by the values and arrive on the correct subfactorial worth. Right here is my answer:

2024_03-Train.c

#embrace <stdio.h>

lengthy factorial(lengthy f)
{
    if( f<=1 )
        return(1);
    else
        return(f*factorial(f-1));
}

lengthy derange(lengthy d)
{
    lengthy r,t;

    r = 0;
    t = factorial(d);
    whereas(d>=0)
    {
        r += (dpercent2 ? -1 : 1)*t/factorial(d);
        d--;
    }

    return(r);
}

int major()
{
    lengthy a;

    for(a=0; a<14; a++)
        printf("!%ld = %ldn",a,derange(a));

    return 0;
}

My code makes use of lengthy integers all through. Sure, I initially used the int information sort, but it surely’s too slender to acquire the bigger values.

The major() perform loops by values zero by 13, calling the derange() perform in a printf() assertion.

The derange() perform obtains the factorial of the worth handed, d. Then a whereas loop works by the equation flipping between constructive and unfavorable values multiplied by the factorial of the unique worth of d and divided by the present factorial of d. This expression is how I interpret the equation from Determine 1. The result’s returned in variable r.

The factorial() perform is recursive, mirroring a submit I wrote some time again. I did replace the code in order that the if take a look at evaluates f, which accounts for !0.

Here’s a pattern run:

!0 = 1
!1 = 0
!2 = 1
!3 = 2
!4 = 9
!5 = 44
!6 = 265
!7 = 1854
!8 = 14833
!9 = 133496
!10 = 1334961
!11 = 14684570
!12 = 176214841
!13 = 2290792932

These are the values you have to see to gauge your answer’s success.

My answer is just one strategy, and the equation I take advantage of is just one option to reveal subfactorials. I hope your answer is profitable, however that you simply additionally loved coding it as a lot as I did mine.