What’s AA? » Cleve’s Nook: Cleve Moler on Arithmetic and Computing

I’ve been explaining our backslash operator for nearly 50 years, however I’ve to confess that the title of right now’s weblog publish appears a bit unusual. You by no means see 33 for numbers. So, what’s AA ?

AA solves the equation

   |A*X = A|

If A is sq. and nonsingular, then X = I. However what if A is rectangular, or singular, or not recognized precisely? These are all nontrivial questions.

This publish is my response to a latest inside dialogue at MathWorks about backslash producing NaNs.

Any common assertion about matrices must be relevant to 1-by-1 matrices particularly. For 1-by-1 matrices, there’s a straightforward reply to our query.

My colleague Pete Stewart likes to make use of “mono-elemental” for this vital class of matrices.

When the 1-by-1 case is generalized to n-by-n with bigger n, it turns into:

This isn’t the top of the story, in fact. It is our job to research roughly nonsingular and roughly equals.

When my daughter was within the fifth grade, her math trainer instructed her that mathematicians hadn’t found out but methods to divide by zero. However the authors of the IEEE 754 customary for floating level arithmetic have figured it out and have assured us that 0 is just not equal to 1, however reasonably

And, for a diagonal matrix of any order, this scalar case is relevant to every diagonal factor.

If A is a rank poor matrix with rank r < n, then AA can’t presumably be I. The rank of the product of two matrices can’t be bigger than rank of both matrix. So AA can’t outrank A itself and

Listed below are three examples the place AA generates NaN .

     A = 0
     B = [1 0; 0 0]
     C = [1 2; 4 8]

     X = AA
     Y = BB
     Z = CC

A =

     0


B =

     1     0
     0     0


C =

     1     2
     4     8


X =

   NaN


Y =

     1     0
   NaN   NaN


Z =

   NaN   NaN
   NaN   NaN

I at all times like to research any property of matrices by testing magic squares.

    small_fig
    warning off
    nmax = 50;
    r = zeros(nmax,1);
    e = zeros(nmax,1);

    for n  = 1:nmax
        A = magic(n);
        X = AA;
        I = eye(n);
        r(n) = rank(A);
        e(n) = norm(X-I);
    finish

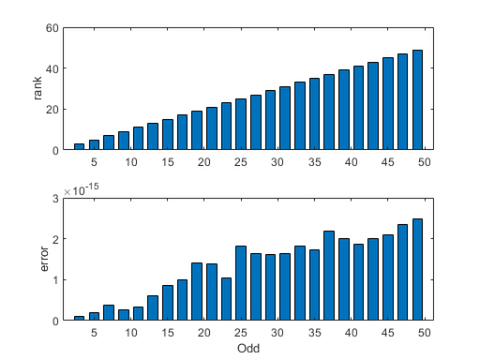
MATLAB makes use of three completely different algorithms for computing magic squares, odd, singly even and doubly even. If the order n is odd, then A = magic(n) is nonsingular, the rank of A is n and the weather of the computed AA are inside roundoff error of the weather of I. Discover that the size issue for the error plot is 3.0e-15.

    n = 3:2:nmax;
    plots(n,r,60,e,[],"Odd")

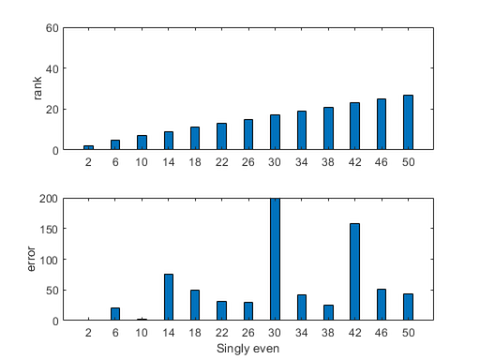
If the order n is divisible by 2, however not by 4, then magic(n) is rank poor. Its rank is about half its order. The error plot displays the truth that AA is just not I.

    n = 2:4:nmax;
    plots(n,r,60,e,200,"Singly even")

If the order n is divisible by 4, then magic(n) could be very rank poor. The rank is at all times 3. The error plots are far and wide. Orders 8 and 40 have errors which are bigger than my plot scale. Orders 16 and 32 are lacking fully as a result of computing AA encounters 0 leading to NaN.

    n = 4:4:nmax;
    plots(n,r,12,e,750,"Doubly even")

Is pinv(A)*b extra “sturdy” than Ab?

You shouldn’t use pinv simply to create options to issues that should not have options. The pseudoinverse is meant to characterize the answer to a selected technical query: if a system of linear equations has many options, which is the shortest one? In the event you substitute Ab by pinv(A)*b, ensure that is what you need.

Utilizing pinv as a substitute of backslash doesn’t get rid of rank deficiency. The difficulties are already current in mono-elemental matrices. The one rank poor 1-by-1 matrix is 0 and pinv(0) = 0. That is much less in-your-face than NaN, however there isn’t any means you can also make pinv(0)*0 equal to 1.

Once I redo the examples above, I get

     A = 0
     B = [1 0; 0 0]
     C = [1 2; 4 8]

     X = pinv(A)*A
     Y = pinv(B)*B
     Z = pinv(C)*C

A =

     0


B =

     1     0
     0     0


C =

     1     2
     4     8


X =

     0


Y =

     1     0
     0     0


Z =

    0.2000    0.4000
    0.4000    0.8000

The NaNs are gone, however is that this actually “extra sturdy” than backslash? In the event you nonetheless suppose so, clarify the place Z comes from.

This has been about sq., dense, nonsymmetric matrices A. For such matrices: