As a mechanical engineer, I really like simulating bodily phenomena. When you’ve got equations of movement, you’ll be able to simply simulate it in MATLAB utilizing ode solvers. After all, you too can simulate dynamic techniques with Simulink or with our bodily modeling instruments. With ode solvers, you’ll be able to detect occasions to simulate issues like a bouncing ball. (By the way in which, here is an instance of a bouncing ball simulated utilizing Simulink).
After I noticed this simulation of a bouncing rod by Matthew, it introduced me a smile. It is a good extension to the bouncing ball simulator:
- The rod strikes in 2 dimensions. Positional states embody $ left[x, y, dot{x}, dot{y}right] $
- The rod also can rotate. Rotational states embody $ left[theta, dot{theta}right] $
- Collision (contact) with the bottom can occur in a number of circumstances: high tip of the rod hitting the bottom, backside tip of the rod hitting the bottom, or the rod hitting the bottom (largely) parallel to the bottom. Based mostly on the state of affairs, the brand new states for the rod are calculated.
- There are two completely different modes of operation: flight and sliding. Usually the rod is in flight mode. When the rod reaches a sure state, it will definitely switches to sliding mode.
As soon as the simulation finishes, it reveals the animation of the dynamics.
It is a nice instance to know the idea of ODE solvers and the occasion dealing with functionality of the solvers. This serves the aim of instructing thoses ideas. There are, nevertheless, a few extra results that may very well be added to this simulation to make it much more true to the physics.
- Add friction – you’ll be able to see this particularly as soon as the rod goes into sliding mode. The rod retains sliding eternally. Including frictional forces to slidingPhase.m can accomplish this.
- Enhance the switching logic for sliding – presently, the rod switches to sliding mode when it detects the middle of mass (COM) is near the bottom. This logic signifies that when the COM is near zero, the rod is close to parallel to the bottom. This can be an affordable logic for many circumstances. Nonetheless, it does not precisely characterize a case the place the rod falls down flat on the bottom with vertical pace. In actuality, the rod will bounce up because of affect, however the simulation switches to sliding on this case. This is an instance of a case the place the rod falls parallel to the bottom. One method could be to have a look at not simply the COM but additionally the vertical pace of the rod. One other method is to calculate the states after collision, and swap to sliding mode if the vertial pace is under a threshold.
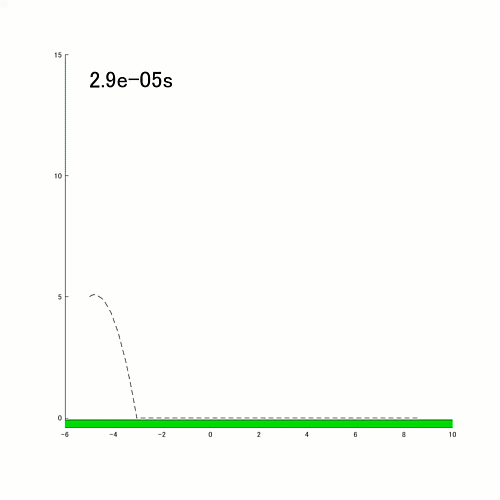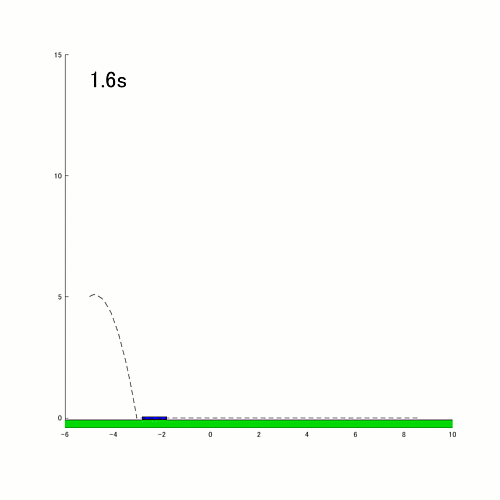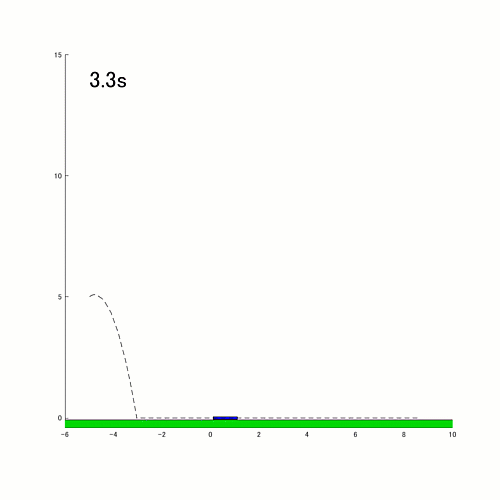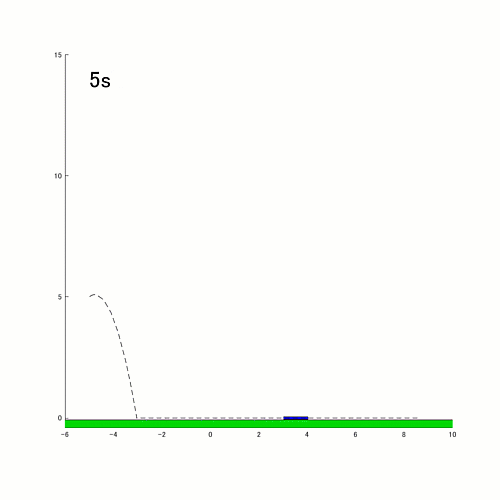
These are enchancment concepts, however these do not take away any of the worth this entry supplies to individuals desirous to simulate dynamic techniques with occasion dealing with.
Feedback
Very effectively achieved, Matthew! Give this a try to tell us what you assume right here or go away a remark for Matthew.
